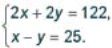Як обчислити периметр чотирикутника?
Для того, щоб обчислити периметр чотирикутника  зі сторонами
зі сторонами  ,
,  ,
,  та
та  , потрібно знайти суму довжин цих сторін, тобто
, потрібно знайти суму довжин цих сторін, тобто  , де
, де  – периметр чотирикутника.
– периметр чотирикутника.
 зі сторонами
зі сторонами  ,
,  ,
,  та
та  , потрібно знайти суму довжин цих сторін, тобто
, потрібно знайти суму довжин цих сторін, тобто  , де
, де  – периметр чотирикутника.
– периметр чотирикутника.Зауваження: якщо позначити довжини сторін чотирикутника буквами  ,
,  ,
,  і
і  , то формула периметра чотирикутника перепишеться у більш звичній буквенній формі:
, то формула периметра чотирикутника перепишеться у більш звичній буквенній формі:  .
.
 ,
,  ,
,  і
і  , то формула периметра чотирикутника перепишеться у більш звичній буквенній формі:
, то формула периметра чотирикутника перепишеться у більш звичній буквенній формі:  .
.Периметр чотирикутника – розв’язування прикладів.
Приклад 1: сторони  ,
,  ,
,  та
та  чотирикутника
чотирикутника  дорівнюють
дорівнюють  ,
,  ,
,  і
і  відповідно. Знайдіть перимет чотирикутника.
відповідно. Знайдіть перимет чотирикутника.
 ,
,  ,
,  та
та  чотирикутника
чотирикутника  дорівнюють
дорівнюють  ,
,  ,
,  і
і  відповідно. Знайдіть перимет чотирикутника.
відповідно. Знайдіть перимет чотирикутника.Отже, для отримання відповіді складемо всі сторони:  .
.
 .
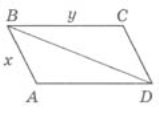
.Приклад 2: у чотирикутник  вписано коло,
вписано коло,  ,
,  . Знайдіть периметр чотирикутника.
. Знайдіть периметр чотирикутника.
 вписано коло,
вписано коло,  ,
,  . Знайдіть периметр чотирикутника.
. Знайдіть периметр чотирикутника.Для чотирикутника описаного навколо кола справедлива рівність:  . Отже, периметр можна обчислити як
. Отже, периметр можна обчислити як  .
.
 . Отже, периметр можна обчислити як
. Отже, периметр можна обчислити як  .
.Приклад 3: знайдіть сторони чотирикутника, якщо його периметр дорівнює  , а довжина кожної сторони, починаючи з другої, на
, а довжина кожної сторони, починаючи з другої, на  більша за довжину попередньої.
більша за довжину попередньої.
 , а довжина кожної сторони, починаючи з другої, на
, а довжина кожної сторони, починаючи з другої, на  більша за довжину попередньої.
більша за довжину попередньої.Отже, позначимо сторону  чотирикутника
чотирикутника  через
через  . Тоді, за умовою,
. Тоді, за умовою,  ,
,  і
і  .
.
 чотирикутника
чотирикутника  через
через  . Тоді, за умовою,
. Тоді, за умовою,  ,
,  і
і  .
.Далі, виходячи з того, що периметр чотирикутника дорівнює сумі довжин кожної його сторони, матимемо:  .
.
 .
.Звідси, довжини сторін  ,
,  ,
,  та
та  заданого чотирикутника дорівнюють
заданого чотирикутника дорівнюють  ,
,  ,
,  і
і  відповідно.
відповідно.
 ,
,  ,
,  та
та  заданого чотирикутника дорівнюють
заданого чотирикутника дорівнюють  ,
,  ,
,  і
і  відповідно.
відповідно.Блок-схема алгоритму знаходження периметра чотирикутника